こちらの続きです。
曲線と戦ってみる4 - C#ATIA
色々な曲線を試しているうちに気が付くのですが、
このマクロ欠点が幾つか有ります。
・直線部分は近似化されない
直線部は、3点通過の円弧が作成出来ない為当然と言えば
当然です。
こんな感じで直線が含まれた曲線に対し、マクロを実行。
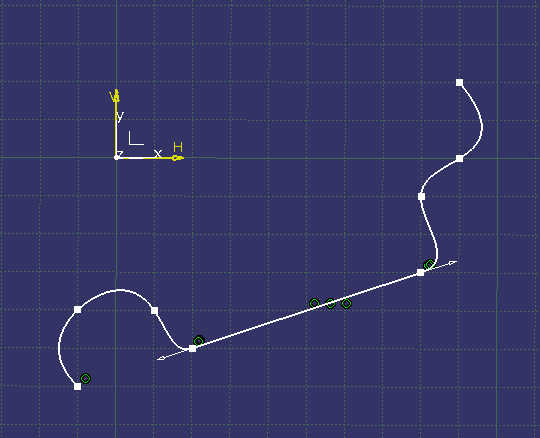
水色部分は近似化されましたが、白色部は近似化されて
いません。
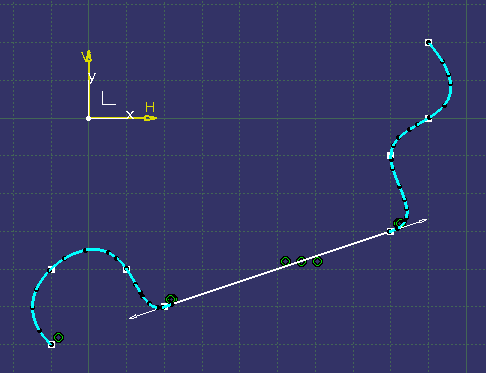
トレランス以内で直線として近似化できるのであれば、
直線を作ってしまっても良いのかなぁ? とは思っています。
が、後回しにします。
・曲線長さとトレランスと分割点との関係
例えばこんな曲線に対し、マクロを実行します。
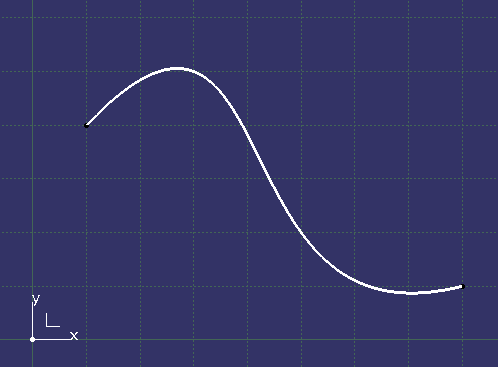
こんな感じで、無事処理できます。
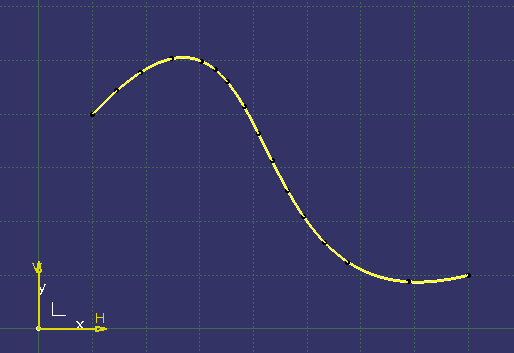
元の曲線を1000倍にして、処理を行うとこんな
感じです。

緑が近似化した円弧郡です。 白い部分は近似化出来ていません。
特にType2のマクロでは、こんなエラーが出てきます。
再帰の回数が多すぎる為に出てくるエラーなのだろうと思います。
又、近似化出来ない部分が出てくるだけが問題ではありません。
1000倍したものを近似化した状態を拡大すると、
このような感じになっています。

多くの円弧が連続した3点で作成されています。実は連続した3点で
出来上がっている円弧は、トレランスを満たしていない可能性があります。
仮に、曲線とチャレンジする円弧がこのような状態だとします。
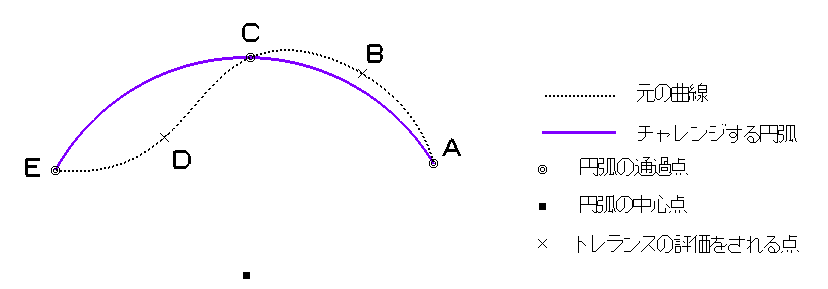
円弧はACEを通過するように作成している為、トレランス以内に近似化
する為の処理は、現状両端を除いたBCDで評価されます。
ところが、連続した3点で作成されている円弧は、BとDが無い状態と
なる為、評価される点はCだけとなります。 もちろんCは円弧作成に
使用されている点の為、当然トレランスを満たした状態となっています。
極端な話、連続した3点では無条件(直線に近い状態は除く)で円弧が
作成されていると言う事になります。
実際に確認してみると、トレランスを満たしていない状態で近似化されて
いる部分が幾つか見られました。
(95000mmぐらいの曲線を、0.02mm以内で近似化させる事が現実的では
無いと思いますが・・・)
これを解決する為には、点の数の固定を止め、曲線の長さ・状態と
トレランスから、最適な点の数を求めれば、改善できるのではないのかな?
と思っています。 最適な点の数ってどうやって求めれば良いのだろう?