曲線と戦ってみる9

曲線の長さとﾁｬﾚﾝｼﾞする円弧の長さの関係を
掴みたい為、こちらのｺｰﾄﾞを修正しました。
曲線と戦ってみる4 - C#ATIA

何処を修正したのか忘れてしまった為、全てｺｰﾄﾞを
記載しておきます。(KCLは必要です)

'vba Arc_Approximated2
Option Explicit

Private Const mPntCount = 301&          '曲線上のﾎﾟｲﾝﾄ数
Private Const mIndexMax = mPntCount - 1 '配列用のｲﾝﾃﾞｯｸｽ最大値
Private Const mTole = 0.02              '近似ﾄﾚﾗﾝｽ
Private Const PI = 3.141592             '円周率 4 * Math.Atn(1)
Private mPnts As Variant                '曲線上の点
Private mPoss As Variant                '曲線上の点の座標値
Private mArcs() As Variant              '近似化成功した際の3点のｲﾝﾃﾞｯｸｽ
Private mArcsCount&                     '近似化成功した数
Private mCurveLen#                      '選択した曲線長さ

Sub CATMain()
    'Documentﾁｪｯｸ
    If KCL.IsType_Of_T(CATIA.ActiveDocument, "DrawingDocument") Then
        MsgBox "Part又はProductﾌｧｲﾙを開いてください"
        Exit Sub
    End If
    
    '曲線選択
    Dim Msg$: Msg = "曲線を選択して下さい : ESCｷｰ 終了"
    Dim SelElem As SelectedElement
    Set SelElem = KCL.SelectElement(Msg, Array("HybridShape"))
    If KCL.IsNothing(SelElem) Then Exit Sub
    Dim CurveRef As Reference: Set CurveRef = SelElem.Reference
    
    '各種設定
    Dim Doc As PartDocument: Set Doc = KCL.GetParent_Of_T(CurveRef, "PartDocument")
    
    '点作成、座標値取得
    mPnts = InitPntsOnCurve(Doc.Part, CurveRef)
    mPoss = GetCoordinatesAry(mPnts)
    
    '近似化
    mCurveLen = GetCurveLength(Doc.Part, CurveRef)
    ReDim mArcs(mIndexMax)
    mArcsCount = 0
    Debug.Print "曲線全長,点数,ﾄﾚﾗﾝｽ" + vbNewLine + _
                CStr(mCurveLen) + "," + CStr(mPntCount) + "," + CStr(mTole) + vbNewLine + _
                "曲線長さ,円弧長さ,近似化" '検証
    Call ChallengeArc(0, mIndexMax)
    If mArcsCount < 1 Then
        MsgBox "近似化できませんでした"
        '本当は点を削除する必要性アリ
        Exit Sub
    End If
    ReDim Preserve mArcs(mArcsCount - 1)
    
    '点群出力
    Call AddTreePnts(mPnts, Doc.Part, "Points")
    
    '近似生成
    Dim ArcCount&: ArcCount = Init3PntArc(mArcs, Doc.Part, "ConvertArcs")
    
    'end
    MsgBox "円弧を" + CStr(ArcCount) + "個生成"
End Sub


'----- ｻﾎﾟｰﾄ関数 -----
'近似化の生成
'return-形状ｾｯﾄ内の要素数
Private Function Init3PntArc&(ByVal Ary As Variant, ByVal Pt As Part, ByVal HBName As String)
    Dim Fact As HybridShapeFactory: Set Fact = Pt.HybridShapeFactory
    Dim Ref(2) As Reference
    Dim Arc() As HybridShapeCircle3Points: ReDim Arc(UBound(Ary))
    Dim i&
    On Error Resume Next
    For i = 0 To UBound(Ary)
        Set Arc(i) = Fact.AddNewCircle3Points(mPnts(Ary(i)(0)), _
                                              mPnts(Ary(i)(1)), _
                                              mPnts(Ary(i)(2)))
        Call Pt.UpdateObject(Arc(i))
        If Not Err.Number = 0 Then
            '演算上OKでもCATIAのﾄﾚﾗﾝｽ上NGとなるﾃﾞｰﾀを除去
            Set Arc(i) = Nothing
            Err.Clear
        End If
    Next
    On Error GoTo 0
    Init3PntArc = AddTreePnts(Arc, Pt, HBName)
End Function

'形状ｾｯﾄに挿入
'return-形状ｾｯﾄ内の要素数
Private Function AddTreePnts&(ByVal Ary As Variant, ByVal Pt As Part, ByVal HBName As String)
    Dim HB As HybridBody: Set HB = Pt.HybridBodies.Add
    HB.Name = HBName
    Dim i&
    For i = 0 To UBound(Ary)
        If Not KCL.IsNothing(Ary(i)) Then
            Call HB.AppendHybridShape(Ary(i))
        End If
    Next
    AddTreePnts = HB.HybridShapes.Count
End Function

'ﾄﾚﾗﾝｽ以内に近似化可能な3点のｲﾝﾃﾞｯｸｽ郡を取得 - 再帰
Private Sub ChallengeArc(ByVal StIdx&, ByVal EndIdx&)
    If 2 > (EndIdx - StIdx) Then
        Exit Sub
    End If
    Dim MidIdx&: MidIdx = Int((StIdx + EndIdx) * 0.5)
    Dim Arc As Variant
    Arc = GetCircumCircleOfTriangle(mPoss(StIdx), mPoss(MidIdx), mPoss(EndIdx))
    
    Dim CLen$: CLen = CStr(mCurveLen * ((EndIdx - StIdx) / mIndexMax)) '検証
    
    If Not IsEmpty(Arc) Then
        If CheckTolerance(KCL.GetRangeAry(mPoss, StIdx + 1, EndIdx - 1), Arc) Then
            'OK
            Debug.Print CLen + " , " + CStr(Arc(2)) + " , OK" '検証
            mArcs(mArcsCount) = Array(StIdx, MidIdx, EndIdx)
            mArcsCount = mArcsCount + 1
            Exit Sub
        Else
            Debug.Print CLen + " , " + CStr(Arc(2)) + " , NG" '検証
        End If
    Else
        Debug.Print CLen + " ,  , NG"  '検証
    End If
    'NG
    Call ChallengeArc(StIdx, MidIdx)
    Call ChallengeArc(MidIdx, EndIdx)
End Sub

'座標値郡が円弧のﾄﾚﾗﾝｽ以内に有るかﾁｪｯｸ
'GetCircumCircleOfTriangle関数の戻り値を使用すること
Private Function CheckTolerance(ByVal Ary As Variant, ByVal Arc As Variant) As Boolean
    Dim i&
    For i = 0 To UBound(Ary)
        If mTole < Math.Abs(Arc(1) - GetDist(Ary(i), Arc(0))) Then
            CheckTolerance = False
            Exit Function
        End If
    Next
    CheckTolerance = True
End Function

'点群より座標値郡取得
Private Function GetCoordinatesAry(ByVal Pnts As Variant) As Variant
    Dim Poss() As Variant: ReDim Poss(mIndexMax)
    Dim P(2) As Variant, i&
    For i = 0 To mIndexMax
        Call Pnts(i).GetCoordinates(P)
        Poss(i) = P
    Next
    GetCoordinatesAry = Poss
End Function

'曲線上の点群作成
Private Function InitPntsOnCurve(ByVal Pt As Part, ByVal CurveRef As Reference) As Variant
    Dim Fact As HybridShapeFactory: Set Fact = Pt.HybridShapeFactory
    Dim Pnts() As Variant: ReDim Pnts(mIndexMax)
    Dim i&, Ratio#
    For i = 0 To mIndexMax
        Ratio = i / mIndexMax
        Set Pnts(i) = Fact.AddNewPointOnCurveFromPercent(CurveRef, Ratio, False)
        Call Pt.UpdateObject(Pnts(i))
    Next
    InitPntsOnCurve = Pnts
End Function

'曲線長さの取得
Private Function GetCurveLength#(ByVal Pt As Part, ByVal Ref As Reference)
    GetCurveLength = Pt.Parent.GetWorkbench("SPAWorkbench").GetMeasurable(Ref).Length
End Function


'----- 演算関連 -----
'三角形の外接円の取得(3点通過円)
'return:array(0)-外心(array(2))
'       array(1)-半径
'       array(2)-円弧長さ
Private Function GetCircumCircleOfTriangle(ByVal P1 As Variant, _
                                           ByVal P2 As Variant, _
                                           ByVal P3 As Variant) As Variant
    Dim M1 As Variant: M1 = GetMidPnt(P1, P2)
    Dim M2 As Variant: M2 = GetMidPnt(P2, P3)
    
    Dim V1 As Variant: V1 = Normalize(ToVecter(P1, P2))
    Dim V2 As Variant: V2 = Normalize(ToVecter(P2, P3))
    
    Dim PlaneVec As Variant '3P平面のﾍﾞｸﾄﾙ
    PlaneVec = Cross(V1, V2)
    Dim EulerLineVec As Variant 'V2の直交ﾍﾞｸﾄﾙ
    EulerLineVec = Normalize(Cross(V2, PlaneVec))
    
    '3点が直線上に存在している場合、除去
    Dim nv#: nv = Dot(V1, EulerLineVec)
    If GetDistSquare(ZeroVec, EulerLineVec) < 0.001 Then Exit Function
    If Math.Abs(nv) < 0.001 Then Exit Function 'ｵﾘｼﾞﾅﾙは過剰な精度な為値を修正
    
    'これが何に該当するのか不明 M2から外心までの距離？
    Dim t#: t = (Dot(V1, M1) - Dot(V1, M2)) / nv
    
    '外接円
    Dim CCofT(2) As Variant
    CCofT(0) = GetCircumCenter(M2, EulerLineVec, t)             '外心取得
    CCofT(1) = GetDist(CCofT(0), P1)                            '半径取得
    Dim Over180 As Boolean '円弧の開き180°を超えているか？
    Over180 = IIf(Dot(Normalize(Cross(Normalize(ToVecter(P1, P3)), PlaneVec)), _
                  Normalize(ToVecter(P1, CCofT(0)))) > 0, True, False)
    CCofT(2) = GetArcLength(CCofT(1), GetDist(P1, P3), Over180) '円弧長さ
    GetCircumCircleOfTriangle = CCofT
End Function

'2点の中間点
Private Function GetMidPnt(ByVal P1 As Variant, ByVal P2 As Variant) As Variant
    Dim Pnt(2) As Double, i&
    For i = 0 To UBound(Pnt)
        Pnt(i) = (P1(i) + P2(i)) * 0.5
    Next
    GetMidPnt = Pnt
End Function

'外心の取得
Private Function GetCircumCenter(ByVal P As Variant, _
                                 ByVal V As Variant, _
                                 ByVal L As Double) As Variant
    Dim cc(2) As Double, i&
    For i = 0 To UBound(cc)
        cc(i) = P(i) + V(i) * L
    Next
    GetCircumCenter = cc
End Function

'2点間距離-平方数
Private Function GetDistSquare#(ByVal P1 As Variant, ByVal P2 As Variant)
    GetDistSquare = (P2(0) - P1(0)) * (P2(0) - P1(0)) + _
                    (P2(1) - P1(1)) * (P2(1) - P1(1)) + _
                    (P2(2) - P1(2)) * (P2(2) - P1(2))
End Function

'2点間距離
Private Function GetDist#(ByVal P1 As Variant, ByVal P2 As Variant)
    GetDist = Math.Sqr(GetDistSquare(P1, P2))
End Function

'半径と弦の長さより円弧の長さを取得
'param:Radius-半径,Chord-弦の長さ,Over-180°越え？
'return:円弧長さ
Private Function GetArcLength#(ByVal Radius As Double, ByVal Chord As Double, _
                               ByVal Over As Boolean)
    Dim Theta#: Theta = ASin((Chord / 2) / Radius) * 2
    GetArcLength = Radius * IIf(Over, 2 * PI - Theta, Theta)
End Function

'ｱｰｸｻｲﾝ
Private Function ASin#(Number As Double)
    Dim X#, Y#, Z#
    '辺Zに仮定値を与えて辺Xと辺Yの値を算出
    Z = 1#
    Y = Z * Number
    X = Math.Sqr(Z * Z - Y * Y)
    
    'ラジアンを取得
    Select Case Number
    Case -1
        '正弦=-1の場合は-90度
        ASin = (PI / 2) * -1
    Case 1
        '正弦= 1の場合は 90度
        ASin = (PI / 2) * 1
    Case Else
        'YとXの正接(tanθ=Y / X)からラジアンを取得
        ASin = Math.Atn(Y / X)
    End Select
End Function


'----- ﾍﾞｸﾄﾙ関連 -----
'内積3D
Private Function Dot(ByVal V1 As Variant, ByVal V2 As Variant) As Double
    Dot = V1(0) * V2(0) + V1(1) * V2(1) + V1(2) * V2(2)
End Function

'外積3D
Private Function Cross(ByVal V1 As Variant, ByVal V2 As Variant) As Variant
    Dim Vec(2) As Double
    Vec(0) = V1(1) * V2(2) - V1(2) * V2(1)
    Vec(1) = V1(2) * V2(0) - V1(0) * V2(2)
    Vec(2) = V1(0) * V2(1) - V1(1) * V2(0)
    Cross = Vec
End Function

'単位ﾍﾞｸﾄﾙ化
Private Function Normalize(ByVal V1 As Variant) As Variant
    Dim L As Double: L = GetDist(ZeroVec, V1)
    If L < 0.00001 Then
        Normalize = ZeroVec
        Exit Function
    End If
    Dim Nml(2) As Double, i&
    For i = 0 To UBound(Nml)
        Nml(i) = V1(i) / L
    Next
    Normalize = Nml
End Function

'2点間ﾍﾞｸﾄﾙ
Private Function ToVecter(ByVal P1 As Variant, ByVal P2 As Variant) As Variant
    Dim Vec(2) As Double, i&
    For i = 0 To UBound(Vec)
        Vec(i) = P2(i) - P1(i)
    Next
    ToVecter = Vec
End Function

'ｾﾞﾛﾍﾞｸﾄﾙ
Private Function ZeroVec() As Variant
    ZeroVec = Array(0#, 0#, 0#)
End Function

主にChallengeArc関数でｲﾐﾃﾞｨｴｲﾄｳｨﾝﾄﾞｳに曲線、円弧の長さ
成功失敗の結果を出力させています。

実はこれちょっと前に出来上がっていたのですが、円弧長さの
計算が正しいものか自信が無く･･･。
検索すればｽﾞﾊﾞｯと式が見つかると思ったのですが、見つからず。
結局、裏紙に丸と三角書いて考えました。
f:id:kandennti:20160623132948p:plain
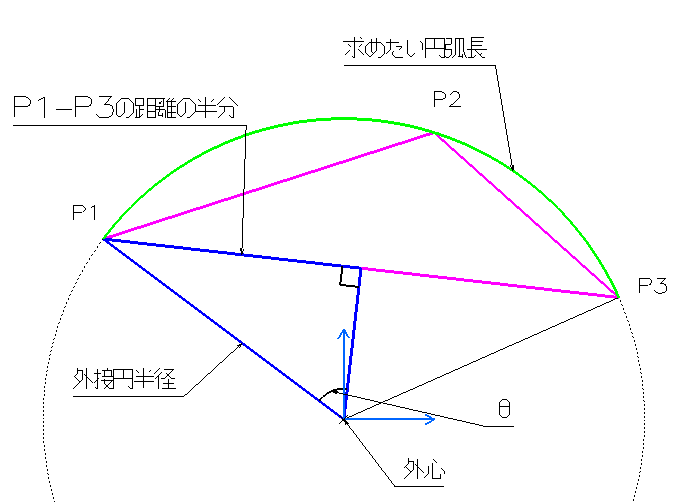
通過する3点をﾋﾟﾝｸの三角形とみなし外接円は既にわかっています。
P1-外心-P3の角度が求まればよいわけです。
外接円半径とP1-P3距離の半分を利用し、ｱｰｸｻｲﾝでθを算出し
円弧長さを求めました。(もっとすんなり計算する方法有りますか?)